Let's consider a normal line that is perpendicular to the curve in the first quadrant at the abcissa

. Being locally perpendicular to the curve, its slope is perpendicular to the curve's local slope, which is its derivative at

. The derivative of
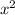
is
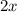
hence the curve's local slope at that point is
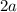
. As a result, the normal line's slope is
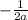
. The normal line's curve's equation is thus of the form
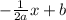
. What is more, its value at

is
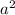
hence

thus
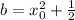
.
Hence the equation of the normal line is
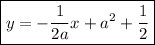
Let's proceed to finding where it intercept the curve in the second quadrant. We have to solve
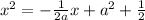
. This equation's discriminant is
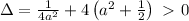
. This yields two solutions

, one of which is negative (and hence in the second quadrant), that is

.
The "extreme normal line" is the one for which that absissa is the greatest (i.e. the closest to

since they're negative). Let us this derive
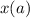
with respect to

:
![x'(a)=-\frac{1}2\left[-(1)/(a^2)+\frac{-\frac{8a^3}+8a}{2\sqrt{(1)/(4a^2)+4(a^2+\frac{1}2)}}\right]](https://img.qammunity.org/2016/formulas/mathematics/high-school/3voge5bwkeepgo8e4attwpkju8yda7xv93.png)
.
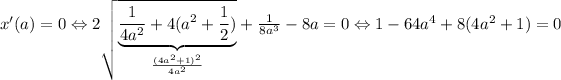
.
Setting
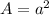
, this leads to
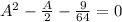
, whose positive root is

. This yields

.
The equation of the extreme normal line is therefore 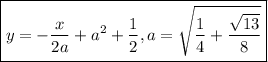
The second question is extremely similar to this one, so I'll just show you the right track :
Let's call
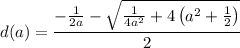
the abcissa of the intersection of a normal ine at

and the curve, which we have computed before. The area between the normal line and the curve is
![\int_(d(a))^ax^2 dx=\left[\frac{x^3}3\right]_(d(a))^a=\frac{1}3\left(a^3-d^3(a)\right)](https://img.qammunity.org/2016/formulas/mathematics/high-school/xzjzgpevod9bifeob14zpbxi4knadru299.png)
. Now, derive this with respect to

in order to find its extrema. You will some
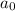
at which it is minimum, and hence the equation of the normal line that traps the least area between itself and the curve will be
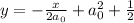
Don't hesitate to ask if you have any question :-) it's a very interesting problem !