Question

A block of wood with a mass of 12.4 kg accelerates to the right with an applied force of 82 N to the right. The coefficient of friction is .2. What is the acceleration of the block?

Answer 1

Procedure:

First, find the weight of the object multiplying its mass times the gravitational acceleration.

Next, identify that the normal force acting on the object is equal to the weight of the object, since there is no vertical acceleration.

Next, remember that the force of friction acting on an object is given by:

`f=\mu N`

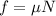
Where μ is the coefficient of friction and N is the normal force acting on the object.

Finally, consider all the forces acting on the object and use Newton's Second Law of Motion to find the acceleration of the object:

`\Sigma\vec{F}=m\vec{a}`

Solution:

The weight W of the object is given by:

`W=mg`

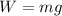
Where m represents the mass of the object and g is the gravitational acceleration on the surface of Earth:

`g=9.81(m)/(s^2)`

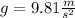
Replace m=12.4kg to find the weight of the object:

The normal force acting on the object has the same magnitude as the weight. Then, substitute μ=0.2 and N=121.644N to find the force of friction:

`\begin{gathered} f=0.2*121.644N \\ \Rightarrow f=24.3288N \end{gathered}`

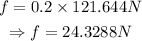
Draw a free body diagram to identify the direction and magnitude of the forces acting on the block:

Let the right direction be represented as positive. The acceleration over the vertical axis is 0, since the forces are balanced. Find the net force over the x-axis:

`\Sigma F_x=82N-24.3288N=57.6712N`

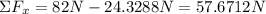
Isolate the acceleration from Newton's Second Law of Motion:

`\begin{gathered} \Sigma F_x=ma_x \\ \Rightarrow a_x=(\Sigma F_x)/(m) \end{gathered}`

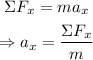
Replace the values of the mass of the block and the net force acting over it to find the acceleration:

Therefore, the acceleration of the block is 4.65 m/s².