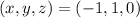Question

Given that the points A=(-1,4,0), B=(2,1,1), C=(2,-2,1) are three vertices of the parallelogram ABCD, findthe fourth vertex D.

Answer 1

GIVEN

A parallelogram ABCD with given vertices

`A=\left(-1,4,0\right),B=\left(2,1,1\right),C=\left(2,-2,1\right)`

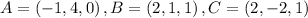
SOLUTION

Let the fourth vertex D have coordinates (x, y, z).

The diagonals of a parallelogram bisect each other. Therefore, the midpoint of the two diagonals must coincide.

For a parallelogram ABCD, the diagonals are AC and BD.

Recall the midpoint formula:

`(x_m,y_m,z_m)=((x_1+x_2)/(2),(y_1+y_2)/(2),(z_1+z_2)/(2))`

Therefore, the midpoint for AC will be:

`AC\Rightarrow((-1+2)/(2),(4+(-2))/(2),(0+1)/(2))=(0.5,1,0.5)`

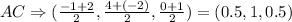
The midpoint of BD will be:

`BD\Rightarrow((2+x)/(2),(1+y)/(2),(1+z)/(2))`

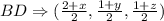
Equate the midpoints:

`((2+x)/(2),(1+y)/(2),(1+z)/(2))=(0.5,1,0.5)`

Therefore:

`\begin{gathered} (2+x)/(2)=0.5,x=-1 \\ (1+y)/(2)=1,y=1 \\ (1+z)/(2)=0.5,z=0 \end{gathered}`

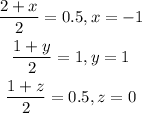
Therefore, the coordinates of the fourth vertex will be:

`(x,y,z)=(-1,1,0)`