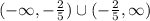Answer:
Explanation:
Given the function:

We are required to find the domain of the given function.
The domain of a rational function are the set of values of x for which the denominator is not equal to 0.
To find the domain of f(x), set the denominator equal to 0 to find the excluded values.
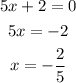
The excluded value in the domain of f(x) is -2/5.
Therefore, the domain of f(x) in interval notation is: