Question

What is the perimeter of thisquadrilateral?31.32 units41.2 units27.7 units50.8 units

Answer 1

We have to calculate the perimeter of the quadrilateral.

The perimeter is the sum of the lengths of the sides.

As we only know the coordinates of the vertices, we will have to calculate the length of each side as the distance between each endpoint.

We will label each vertex as:

(x1,y1) = (2, 6)

(x2,y2) = (4, 1)

(x3,y3) = (-4, -4)

(x4,y4) = (-3, 3)

We can then calculate each distance as:

`\begin{gathered} d_(12)=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d_(12)=√((4-2)^2+(1-6)^2) \\ d_(12)=√(2^2+(-5)^2) \\ d_(12)=√(4+25) \\ d_(12)=√(29) \end{gathered}`
`\begin{gathered} d_(23)=√((x_3-x_2)^2+(y_3-y_2)^2) \\ d_(23)=√((-4-4)^2+(-4-1)^2) \\ d_(23)=√((-8)^2+(-5)^2) \\ d_(23)=√(64+25) \\ d_(23)=√(89) \end{gathered}`
`\begin{gathered} d_(34)=√((x_4-x_3)^2+(y_4-y_3)^2) \\ d_(34)=√((-3-(-4))^2+(3-(-4))^2) \\ d_(34)=√(1^2+7^2) \\ d_(34)=√(1+49) \\ d_(34)=√(50) \end{gathered}`
`\begin{gathered} d_(41)=√((x_1-x_4)^2+(y_1-y_4)^2) \\ d_(41)=√((2-(-3))^2+(6-3)^2) \\ d_(41)=√(5^2+3^2) \\ d_(41)=√(25+9) \\ d_(41)=√(34) \end{gathered}`

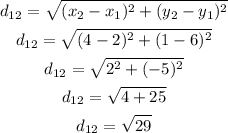
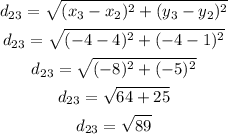
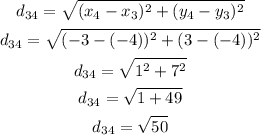
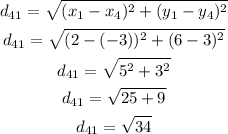
Now we can add the four distances to find the perimeter:

`\begin{gathered} P=d_(21)+d_(32)+d_(43)+d_(14) \\ P=√(29)+√(89)+√(50)+√(34) \\ P\approx5.39+9.43+7.07+5.83 \\ P\approx27.72 \end{gathered}`

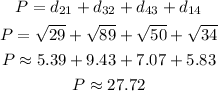
Answer: 27.7 units [Third option]