Question

at green lake, the population of frogs is expected to grow according to the model P(x) = 360(1.1)*, where P(x) is the population of frogs and x is the number of years after 2020. During what year will the population of frogs double?

Answer 1

Let x be the number of years after 2020 such that the population of frogs doubles its number, then we can set the following equation:

`P(x)=2\cdot360.`

Substituting P(x)=360(1.1)^x we get:

`360\mleft(1.1\mright)^x=2\cdot360.`

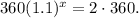
Dividing the above equation by 360 we get:

`\begin{gathered} (360(1.1)^x)/(360)=(2\cdot360)/(360), \\ (1.1)^x=2. \end{gathered}`

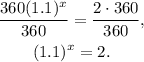
Now, applying the natural logarithm we get:

`\begin{gathered} \ln (1.1^x)=\ln 2, \\ x\ln 1.1=\ln 2. \end{gathered}`

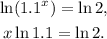
Dividing the above equation by ln1.1 we get:

`\begin{gathered} (x\ln1.1)/(\ln1.1)=(\ln 2)/(\ln 1.1), \\ x=(\ln2)/(\ln1.1)\text{.} \end{gathered}`

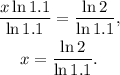
Simplifying the above result we get:

`x\approx7.2425.`

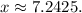
Therefore, during the year 2027, the population of frogs will double its number.

Answer: 2027.