Answer:
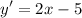
General Formulas and Concepts:
Algebra I
Terms/Coefficients
Functions
Calculus
Limits
Limit Rule [Variable Direct Substitution]:
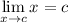
Differentiation
- Derivatives
- Derivative Notation
- Definition of a Derivative:
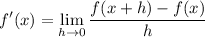
Step-by-step explanation:
Step 1: Define
Identify
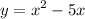
Step 2: Differentiate
- Substitute in function [Definition of a Derivative]:
![\displaystyle y' = \lim_(h \to 0) ([(x + h)^2 - 5(x + h)] - (x^2 - 5x))/(h)](https://img.qammunity.org/2022/formulas/engineering/college/1ag6ygn6zov7jz92o49112n3wysj3g2m0g.png)
- Expand:
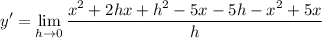
- Combine like terms:
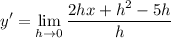
- Factor:
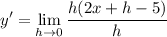
- Simplify:
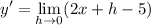
- Evaluate limit [Limit Rule - Variable Direct Substitution]:
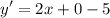
- Simplify:
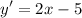
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation