Question

Points A (-10,-6) and B (6,2) are the endpoints of AB. What are the coordinates of point C on AB such that AC is 3/4 the length of AB?

a. (0,-1)
b. (2,0)
c. (-2,-2)
d. (4,1)

Answer 1

The correct answer is:

B) (2,0)

Step-by-step explanation:

First we find the distance of AB using the distance formula:

`d=√((y_2-y_1)^2+(x_2-x_1)^2)`

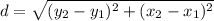
Using the coordinates of A and B, we have:

`image`

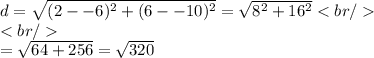
To simplify this radical, we find the prime factorization of 320:

320 = 10*32

10 = 5*2

32 = 16*2

16 = 2*8

8 = 2*4

4 = 2*2

320 = 2*2*2*2*2*2*5

For a square root, we want pairs of factors. There are 3 pairs of 2's, so we take 3 2's out of the radical and leave the 5 in:

`2*2*2√(5)=8√(5)`

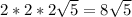
We want the length of AC to be 3/4 of the length of AB:

`(3)/(4)* 8√(5) = (24)/(4)√(5)=6√(5)`

If the coordinates of B are (0, 2), using these and the coordinates of A in the distance formula gives us:

`image`

To simplify this, we find the prime factorization of 180:

180 = 10*18

10 = 5*2

18 = 2*9

9 = 3*3

180 = 3*3*2*2*5

We want pairs. We have a pair of 3's and a pair of 2's; this means a 3 and a 2 come out and the 5 stays in:

`3*2√(5) = 6√(5)`

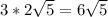
This is the correct length.

Answer 2

B is the correct answer. To find out how long AC is, you must first find the length of AB. To do that, form a triangle by finding the point where perpendicular lines from points A and B meet. According to Pythagoras’ theorem, a^2 + b^2 = c^2. Thus 16^2 + 8^2 = c^2. 256 + 64 = c^2. The square root of this is 17.9. AB is therefore 17.9 units long. 3/4 of 17.9 is 13.4 AC is 13.4 units long. The co ordinate that fits this is (2,0).