Question

A 2.00 m brass rod with a 1.00 mm diameter behaves like a spring under stretching or compression. If the elastic modulus of brass is 9.10 × 1010 N/m2, then the spring constant of the rod is

Answer 1

Given data

*The given length of the rod is l = 2.00 m

*The given diameter of rod is d = 1.0 mm = 1.0 × 10^-3 m

*The elastic modulus of brass is E = 9.10 × 10^10 N/m^2

The formula for the spring constant of the rod is given as

`\begin{gathered} k=(Ea)/(l) \\ =(E*((\pi)/(4)d^2))/(l) \end{gathered}`

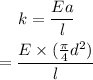
*Here a is the cross-sectional area of the rod

Substitute the known values in the above expression as

`\begin{gathered} k=(9.10*10^(10)*((3.14)/(4)*(1.0*10^(-3))^2))/(2.00) \\ =3.57*10^4\text{ N/m} \end{gathered}`

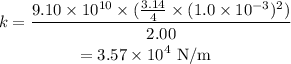
Hence, the spring constant of the rod is k = 3.57 × 10^4 N/m