Question

20. a. The graph of a quadratic function passes

through the point (7,5). The vertex of the
graph is (3, 1). Use symmetry to identify
another point on the function's graph. Explain
your answer.
b. Write the equation of the quadratic function.

PLEASE HELPPP!!!! More points!!!

Answer 1

`\textsf{(a)}\quad (-1, 5)`

`\textsf{(b)} \quad y=(1)/(4)(x-3)^2+1`

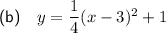
Explanation:

Part (a)

If the vertex of the quadratic function is (3, 1) then the function's axis of symmetry is x=3.

Symmetric points on the curve of a quadratic function have the same y-value and are the same distance (but in opposite horizontal directions) from the axis of symmetry.

The x-value of point (7, 5) is 4 units to the right from the axis of symmetry.

Therefore, the other point that is symmetrical to point (7, 5) has an x-value that is 4 units to the left of the axis of symmetry.

Therefore, another point on the function's graph is:

⇒ (3-4, 5) = (-1, 5)

Part (b)

`\boxed{\begin{minipage}{5.6 cm}\underline{Vertex form of a quadratic equation}\\\\$y=a(x-h)^2+k$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}`

Given information:

• Vertex = (3, 1)
• Point on the curve = (7, 5)

Therefore:

• h = 3
• k = 1
• x = 7
• y = 5

Substitute the values into the formula and solve for a:

`\implies 5=a(7-3)^2+1`

`\implies 5=a(4)^2+1`

`\implies 5=16a+1`

`\implies 4=16a`

`\implies a=(1)/(4)`

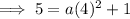
Therefore, the equation of the quadratic function in vertex form is:

`\boxed{y=(1)/(4)(x-3)^2+1}`