Answer:
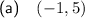
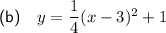
Explanation:
Part (a)
If the vertex of the quadratic function is (3, 1) then the function's axis of symmetry is x=3.
Symmetric points on the curve of a quadratic function have the same y-value and are the same distance (but in opposite horizontal directions) from the axis of symmetry.
The x-value of point (7, 5) is 4 units to the right from the axis of symmetry.
Therefore, the other point that is symmetrical to point (7, 5) has an x-value that is 4 units to the left of the axis of symmetry.
Therefore, another point on the function's graph is:
⇒ (3-4, 5) = (-1, 5)
Part (b)

Given information:
- Vertex = (3, 1)
- Point on the curve = (7, 5)
Therefore:
Substitute the values into the formula and solve for a:
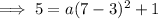
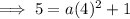



Therefore, the equation of the quadratic function in vertex form is:
