Question

For the function y = 2x^2(a) Find the average rate of change of y with respect to r over the interval [1,4](b) Find the instantaneous rate of change of y with respect to a at the value x = 1.Average Rate of Change= ___Instantaneous Rate of Change at x = 1: _____

Answer 1

Given the function

`y=2x^2`

The formula to find the average rate of change of y with respect to x in [a,b]

`\frac{Change\text{ in y}}{Change\text{ in x}}=(f(b)-f(a))/(b-a)`

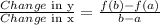
Here, a = 1 and b = 4.

`\begin{gathered} \text{Average rate of change =}(f(4)-f(1))/(4-1) \\ =(2\cdot4^2-2\cdot1^2)/(3) \\ =(30)/(3) \\ =10 \end{gathered}`

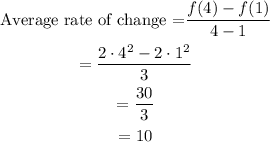
The instantaneous rate of change is the slope of the tangent line at x = 1.

`\begin{gathered} \text{Slope}=(d)/(dx)(2x^2) \\ =2\cdot2x \\ =4x \end{gathered}`

Slope at x = 1 is

`4\cdot1=4`

So, the instantaneous rate of change is 4.