Question

A bus slows down uniformly from 75.0 km/h to 0 km/h in 21 s. How far does it travel before stopping?

Answer 1

1 hour = 3,600 seconds
1 km = 1,000 meters

75 km/hour = (75,000/3,600) m/s = 20-5/6 m/s

The average speed of the bus while it slows down is

(1/2)(20-5/6 + 0) = 10-5/12 m/s .

Traveling at an average of 10-5/12 m/s for 21 seconds,
the bus covers

(10-5/12) x (21) = 218.75 meters .

Answer 2

As per the question,the bus slows down uniformly from 75 km/h to 0 km/h.

Hence the initial velocity of the bus[ u]=75 km/hr.

the final velocity of the bus [v]=0 km/h

the taken by the bus to stop [t]=21 s

we know that 1 km= 1000 m and 1 hour =3600 second.

Hence
`75 km/h =75*(1000 m)/(3600s)`

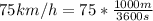
=20.83 m/s

we are asked to calculate the stopping distance.

From equation of kinematics we know that-

v= u +at where a is the acceleration of the particle.

we have v= 0 km/h = 0 m/s and u= 75 km/h =20.83 m/s

t = 21 s

Putting these values in above equation we get-

0 = 20.83 +a×21

⇒ a×21 = -20.83 m/s

⇒a= -[20.83]÷21

`= -0.9919 m/s^2` [ Here negative sign indicates that particle is decelerating ]

Again from the equation of kinematics we know that-

`s = ut +(1)/(2) at^2`

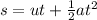
Here s is the distance traveled. Putting the above quantities we get-

`s = 20.83 *21 -(1)/(2) 0.9919 *[21^2]`

s = 218.7 metre. [ans]

Hence the bus will stop after a distance of 218.7 m.