Question

What is the area of the figure?10 feet10 feet2 feet2 feet16 feet40 ft-84 ft296 ft?can't be determined

Answer 1

To find the area of the figure we divide it in two figures like the following picture:

Now, we notice that we have a triangle and a rectangle so we need to find the area of each of them and add them to find the total area.

Since we don't know the height of the triangle but we know its sides we can use Heron's formula:

`A=\sqrt[]{s(s-a)(s-b)(s-c)}`

where s is:

`s=(a+b+c)/(2)`

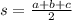
and a, b and c are the lengths of its sides.

Let a=10, b=10 and c=16, then:

`s=(10+10+16)/(2)=18`

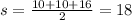
Now that we know s we plug it in the formula for the area:

`\begin{gathered} A=\sqrt[]{18(18-10)(18-10)(18-16)} \\ =\sqrt[]{18\cdot8\cdot8\cdot2} \\ =\sqrt[]{2304} \\ =48 \end{gathered}`

Therefore the area of the triangle is 48 squared feet.

The area of the rectangle is:

`A=bh`

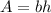
in this case b=16 and h=2, then:

`A=16\cdot2=32`

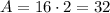
Therefore the area of the figure is 80 squared feet.