Question

Find the value of x.(x + 70° Xo(x + 30°(2x)(2x)(2x - 10°

Answer 1

Given:

The angles of a polygon are (x + 70)°, x°, (x + 30)°, (2x)°, (2x)°, (2x - 10)°.

The number of sides is, n = 6.

The objective is to find the value of x.

The sum of the inner angles of a polygon is, 180(n-2)°.

Then, the value of x can be calculated as,

`\begin{gathered} (x+70)+x+(x+30)+2x+2x+(2x-10)=180\cdot(n-2) \\ x+70+x+x+30+2x+2x+2x-10=180\cdot(6-2) \\ 9x+90=180\cdot(4) \\ 9x+90=720 \\ 9x=720-90 \\ 9x=630 \\ x=(630)/(9) \\ x=70 \end{gathered}`

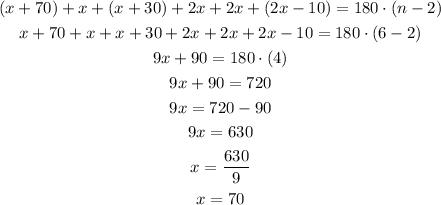
Hence, the value of x is 70.