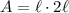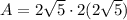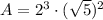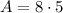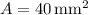Answer and Explanation:
40 square mm
See the attached image.
Basically, the 5mm radius that is given is half the diagonal of the rectangle. So if we double the radius, it becomes the diagonal, which is the hypotenuse of the right triangle that can be constructed of half the rectangle. From there, we can use the Pythagorean theorem to solve for the rectangle's side length by substituting a for
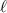 and b for
and b for
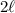 . Finally, we multiply
. Finally, we multiply
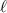 and
and
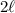 to get the area of the rectangle:
to get the area of the rectangle: