Question

From the base of the tower, you walk 36.37m. From there, you use the clinometer to measure the angle of incline from your eye to the top of the tower, and find out that it is 75 degrees. You measure from the ground to your eye, the distance is 1.63 m. How tall is the tower?

Answer 1

Statement Problem: From the base of the tower, you walk 36.37m.

From there, you use the clinometer to measure the angle of incline from your eye to the top of the tower, and find out that it is 75 degrees. You measure from the ground to your eye, the distance is 1.63 m. How tall is the tower?

Solution:

We would represent the information in a diagram as;

Let T be the height of the tower from the observer's line of sight;

Now, we would apply the trigonometry ratio for tangent;

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan 75^o=(T)/(36.37) \\ T=36.37\tan 75^o \\ T=135.73 \end{gathered}`

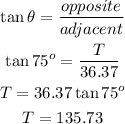
But the height of the tower is the distance from the foot of the tower to the top. Hence, the height of the tower is;

`\begin{gathered} Height\text{ of the tower =}135.73+1.63 \\ Height\text{ of the tower =137.36m} \end{gathered}`

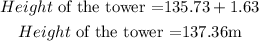
The height of the tower is 137.36m