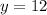Question

Find y when x=15 if y=6 when x=30

Answer 1

The answer is y = 12 when x = 30. You can prove this through some properties of mathematics. Multiply 6 by 2 if x = 30. 30 is two times 15, so it makes sense.
Hope that answered your question.

Answer 2

The problem does not specify whether it is a proportional variation or an inversely proportional variation, so both cases will be solved.

case a) proportional variation

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form

`(y)/(x) =k`

Find the value of k

`y=6\\ x=30\\ k=(6)/(30) =(1)/(5)`

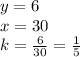
Find the value of y for x=
`15`

`y=kx\\ y=(1)/(5) *15\\ y=3`

the answer case a) is

`y=3`

case b) inverse variation

we know that

A relationship between two variables, x, and y, represent an inverse variation if it can be expressed in the form

`yx =k`

Find the value of k

`y=6\\ x=30\\ k=30*6=180`

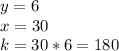
Find the value of y for x=
`15`

`yx=k\\ y=(180)/(15)\\ y=12`

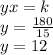
the answer case b) is

`y=12`