Step1: Derive the speed equations from the data.
Given data are as follows
For Dave
Distance traveled = 250 miles
Let the speed of Dave be d miles per hour
For Kent
Distance traveled = 270 miles
Since Kent's speed is 4 miles per hour faster than Dave, we can represent this mathematically
so that If we represent Kent's speed by k. Then
k = 4 + d.
Distance traveled is given by the formula
Distance = Speed x Time
Therefore
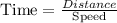
So the time spent by Kent is
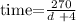
The time spent by Dave is
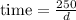
Step 2: Since they both spend the same time, we will equate their time spent
So
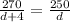
Step3: The next step is to solve the above equation
d (270) = 250 (d+4)
Expand the parenthesis
d x 270 = 250 x d + 250 x 4
270d = 250d + 1000
Collect like terms
270d - 250d = 1000
20d = 1000
Divide both sides by 20
d = 1000/20 = 50
d = 50 miles per hour
So Dave's rate is 50 miles per hour
Since we have been told that Kent travels 4 miles per hour faster than Dave, then
Kent = Dave + 4
K = 50 + 4
k= 54 miles per hour
Hence the rates are
Kent = 54 miles per hour
Dave = 50 miles per hour