Question

Did the period of the pendulum swing depend on the mass of the bob? On the length of the string? How does your data relate to the pendulum equation? You need not include your data tables and graphs, but you should explain your answer based on the information in your data tables and graphs. 30 cm pendulum 25g - 1.05 seconds 50g - 1.01 seconds 100g- 1.03 seconds50 cm pendulum25g- 1.35 s50g- 1.38s100g- 1.40s70 cm pendulum25g- 1.68s50g- 1.61s100g- 1.59S

Answer 1

(1) No the period of the pendulum swing depends on the mass of the bob.

(2) Yes, the period of the pendulum swing did depend on the length of the string.

(3) The data from the experiment is consistent with the pendulum equation.

Question 1:

No, the period of the pendulum swing did not depend on the mass of the bob. We can see this from the fact that the periods for the different masses at each pendulum length are approximately the same. For example, the periods for the 30 cm pendulum are 1.05 seconds for 25 grams, 1.01 seconds for 50 grams, and 1.03 seconds for 100 grams. The differences in period are small and could be due to experimental error.

Question 2:

Yes, the period of the pendulum swing did depend on the length of the string. The longer the string, the longer the period. This can be seen from the fact that the periods for the different lengths of the pendulum at each mass are all different. For example, the periods for the 25 gram bob are 1.05 seconds for a 30 cm pendulum, 1.35 seconds for a 50 cm pendulum, and 1.68 seconds for a 70 cm pendulum.

Question 3:

The pendulum equation is:
`T = \frac{2\Pi{√(L)}}{g}`

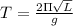
T = 2π√L/g

where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity.

The data from the experiment is consistent with the pendulum equation. For example, if we calculate the period for the 30 cm pendulum using the pendulum equation, we get:

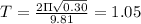`T = \frac{2\Pi{√(0.30)}}{9.81} = 1.05` seconds

This is the same period that we measured for the 30 cm pendulum with a 25 gram bob.

We can do the same calculation for the other pendulum lengths and masses, and we get results that are consistent with the experimental data.

Therefore, the data from the experiment supports the pendulum equation.

Answer 2

We are given that a pendulum has the following half periods for different masses.

For the 30 cm pendulum we have:

`(T_1)/(2)\approx1.0s`

Therefore, the period is determined by multiplying the half period by 2:

`T_1\approx2s`

For the 50 cm pendulum we have that half the period is:

`(T_2)/(2)\approx1.3s`

Therefore, the period is:

`T_2=2.6s`

For the 70 cm pendulum we have that half the period is:

`(T_3)/(2)=1.6s`

The period is:

`T_3=3.2s`

Question 1: Did the period of the pendulum swing depend on the mass of the bob?

We notice that for different masses the period is approximately the same, therefore, the period of the pendulum is independent of the mass.

Question 2: On the length of the string?

The period varies with the length therefore the period is dependent on the length of the pendulum,

Question 3: How does your data relate to the pendulum equation?

The pendulum equation is the following:

`T=2\pi\sqrt{(L)/(g)}`

Where "L" is the length and "g" is the acceleration of gravity.

For the length of "L = 30 cm" we have:

`T=2\pi\sqrt{(0.3m)/(9.8(m)/(s^2))}\approx1s`

For the "L = 50cm" we have:

`T=2\pi\sqrt{(0.5)/(9.8)}\approx1.4s`

For the 70 cm length we have:

`T=2\pi\sqrt{(0.7)/(9.8)}=1.6s`

Therefore, the measurements are consistent with the results of the pendulum equation.