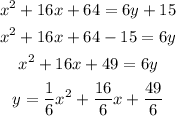Question

Write the equation for a parabola with a focus at (-8,-1) and a directrix at y= -4y =

Answer 1

Since the directrix is y=-4, use the equation of a parabola that opens up or down.

`\mleft(x-h\mright)^2=4p(y-k)`

where vertex is at (h,k) and focus is at (h,k+p)

The vertex is halfway between the directrix and focus. Find the y-coordinate of the vertex using the following

`(-8,(-1-4)/(2))=(-8,-(5)/(2))`

Find the distance from the focus to the vertex.

The distance from the focus to the vertex and from the vertex to the directrix is |p|. Subtract the y-coordinate of the vertex from the y-coordinate of the focus to find p.

`p=-1+(5)/(2)=-(2)/(2)+(5)/(2)=(-2+5)/(2)=(3)/(2)`

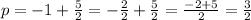
Substitute in the known values for the variables into the equation

`(x-h)^2=4p(y-k)`
`(x+8)^2=4\cdot(3)/(2)\cdot(y+(5)/(2))`

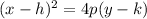
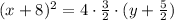
Simplify

`(x+8)^2=6\cdot(y+(5)/(2))`

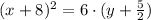
in y=ax^2+bx+c form:

`\begin{gathered} x^2+16x+64=6y+15 \\ x^2+16x+64-15=6y \\ x^2+16x+49=6y \\ y=(1)/(6)x^2+(16)/(6)x+(49)/(6) \end{gathered}`