Question

Convert each geometric sequence into an exponential function. 4, 20, 100, 500,….

Answer 1

`\text{ a}_n=4\cdot(5)^n`

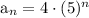
Step-by-step explanation:

here, we want to convert the given geometric sequence into an exponential function

We have the exponential function generally as:

`y=ab^x`

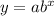
with respect to the geometric sequence, it will be in the form:

`\text{ y = ar}^n`

where a is the first term ,r is the common ration and n is the term number

Looking at the given arrangement, 4 is the first term

Now, we can get the common ratio by dividing subsequent terms

Mathematically, we have that as:

`(100)/(20)\text{ = }(500)/(100)\text{ = }(20)/(4)\text{ = 5}`

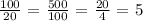
So, we have the first term as 4 and the common ratio as 5

Thus, we have the exponential function as:

`\text{ a}_n=4\cdot(5)^n`

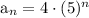
where n is the term number