Question

Identify the pair ofexpressions belowthat are equivalent.7x + 1lyA and1ly + 7xB3x + 3yand 6xy12x – Yc) and6(2x - y)7 + 7 + 7

Answer 1

Pair A:

`7x+11y,11y+7x`

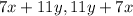
Remember that characteristic of the numbers is that, in general:

`a+b=b+a`

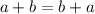
For any numbers a and b, this is always true. So, in our case:

`\begin{cases}a=7x \\ b=11y\end{cases}\Rightarrow7x+11y=11y+7x`

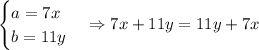
So the pair A is equivalent

As for pair B:

We are going to it by contradiction: if we suppose that the two equations are the same (one is equal to the other) and we found a pair of numbers (x,y) that produce a contradiction, then the two equations cannot be equivalent. Let me show you:

Suppose pair B is equivalent, then:

`3x+3y=6xy`

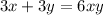
Now, suppose that x=0 and y=1, then:

`3(0)+3(1)=6(0)(1)\Rightarrow3=0!!`

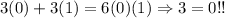
And of course, 3 is not equal to 0!

So, by supposing that the 2 equations are equivalent we reach a false implication, which means that the pair is NOT equivalent

As for pair C:

We can expand the expression 6(2x-y):

`6(2x-y)=6(2x)-6(y)=12x-6y`

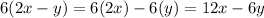
Which is exactly the first expression! So the pair is equivalent!