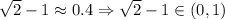

is always non-negative, so the range of
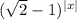
is
![(0,1]](https://img.qammunity.org/2016/formulas/mathematics/high-school/jh6j2po5ua9ho426g98dut4fqwkm0f4m66.png)
The range of
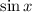
is
![[-1,1]](https://img.qammunity.org/2016/formulas/mathematics/middle-school/o12ixjj6c0cuut6nzf2d38ey7ya6xuuwdf.png)
=> the range of
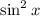
is
![[0,1]](https://img.qammunity.org/2016/formulas/mathematics/high-school/m3vlvzgcreikmxc57y8mcdbk32jilxpie7.png)
=> the range of
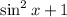
is
![[1,2]](https://img.qammunity.org/2016/formulas/mathematics/high-school/cbeuelmnkzjg3mnneip9dlvxzcyruc93f6.png)
The only common point of these two function is the one with y-coordinate = 1, so

. Let's take one of these functions and find for which x, its value is equal to 1. I'll take the first one.

So,
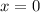
:)