Question

Someone check my work, please :)

Find the inverse:

`f(x)=1.5x^2-4`

My work:

`y=1.5x^2-4\\\\x=1.5y^2-4\\\\x+4=1.5y^2\\\\(x+4)/(1.5) =y^2\\\\y=\sqrt{(x+4)/(1.5) } \\\\f^(-1)(x)=y=\sqrt{(x+4)/(1.5) }`

However, the answer sheet says the answer is
`f^(-1)(x)=\sqrt{(2x+8)/(3) }`. I did notice that if you multiply each number by 2 you get the numbers given in the answers:

`1*2=2\\\\4*2=8\\\\1.5*2=3`

Thanks :)

Answer 1

They are the same. If you were to graph them, they would overlap.

Explanation:

Look at it this way:

`(3)/(2) =1.5`

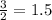
Insert this value:

`f(x)=(3)/(2) x^2-4`

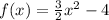
Now solve. Insert y:

`y=(3)/(2)x^2-4`

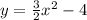
Switch x and y:

`x=(3)/(2)y^2-4`

Add 4 to both sides:

`x+4=(3)/(2)y^2-4+4\\\\x+4=(3)/(2)y^2`

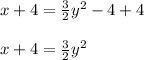
Use the rule
`(a)/(c) b=(ab)/(c)`:

`x+4=(3y^2)/(2)`

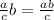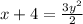
Multiply both sides by 2:

`2(x+4)=2((3y^2)/(2))\\\\2x+8=3y^2`

Divide both sides by 3:

`(2x+8)/(3) =(3y^2)/(3) \\\\(2x+8)/(3)=y^2`

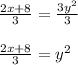
Take the square root of both sides*:

`\sqrt{(2x+8)/(3) } =√(y^2) \\\\y =\sqrt{(2x+8)/(3) } ,-\sqrt{(2x+8)/(3) }`

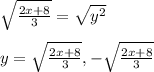
Therefore:

`f^(-1)(x)=\sqrt{(2x+8)/(3) } ,-\sqrt{(2x+8)/(3) }`

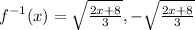
This is not a function (by the way) because ±
`\sqrt{(2x+8)/(3) }` means that there are two y values per x value. If you were to graph this, it would fail the vertical line test, which proves that it is not a function.

:Done

*You need to have the ± symbol when you take a square root because, although 2×2=4, (-2)×(-2)=4 as well. The square root of 4 could be either -2 or positive 2. The same can be said for the above result.