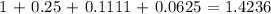Question

Approximate the area under the graph of f(x) over the specified interval by dividing the interval into the indicated number of subintervals and using the left endpoint of each subinterval. f(x) -; interval [1, 5); 4 subintervals x2 O 1.4636 O 1.4236 O 0.4636 0 2.0833

Answer 1

The approximate area under the curve using the left-end points is 1.4236

Here; f(x) = 1/x^2 , [a,b] = [1,5] and n = 4

We start by calculating the width of each of the triangles on the interval

Mathematically, that would be;

`(b-a)/(n)\text{ = }(5-1)/(4)\text{ = 1}`

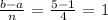
Since there are 4 sub-intervals, there are 4 rectangles

So using the left end-points, we have;

`1\text{ }*\text{ f(1) + (1 }*\text{ f(2)) + (1 }*\text{ f(3)) + (1 }*\text{ f(4))}`

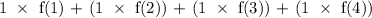
where;

`\begin{gathered} f(1)\text{ = }(1)/(1^2)\text{ = 1} \\ \\ f(2)\text{ = }(1)/(2^2)\text{ = 0.25} \\ \\ f(3)\text{ = }(1)/(3^2)=\text{ }(1)/(9)\text{ = 0.11111} \\ \\ f(4)\text{ = }(1)/(4^2)\text{ = }(1)/(16)\text{ = 0.0625} \end{gathered}`

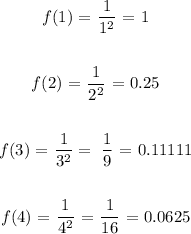
So the approximate area under the curve will be;

`1\text{ + 0.25 + 0.1111 + 0.0625 = 1.4236}`