Question

There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be 36°. From the same location, the angle of elevation to the top of the lightning rod is measured to be 38°. Find the height of the lightning rod. To earn full credit please share a diagram and include all your work and calculations

Answer 1

To better analyze the problem, let us draw an illustration:

To determine the height of the lightning rod, we have to determine the height of the building and the height of the building + lightning rod using the given angles and distance from the base.

Let's solve for the height of the building itself first. Use the 36-degree angle.

`tan36=\frac{height\text{ }of\text{ }the\text{ }building}{distance\text{ }from\text{ }the\text{ }building}`

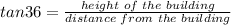
Let's plug in the data to the function above and solve for the height of the building.

`\begin{gathered} tan36=(x)/(500ft) \\ 500tan36=x \\ 363.2713ft=x \end{gathered}`

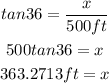
Therefore, the height of the building itself is 363.2713 ft.

Moving on to the height of the building + lightning rod, use the tangent function still but this time, use the 38-degree angle.

`\begin{gathered} 500tan38=x \\ 390.6428=x \end{gathered}`

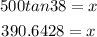
Therefore, the height of the building + lightning rod is 390.6428ft.

So, to determine the height of the lightning rod only, let's subtract the two calculated heights.

`\begin{gathered} lightning\text{ }rod=390.6428ft-363.2713ft \\ lightning\text{ }rod=27.3715\approx27.37ft \end{gathered}`

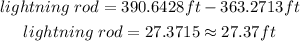
Answer:

The height of the lightning rod is approximately 27.37 ft.