To better analyze the problem, let us draw an illustration:
To determine the height of the lightning rod, we have to determine the height of the building and the height of the building + lightning rod using the given angles and distance from the base.
Let's solve for the height of the building itself first. Use the 36-degree angle.
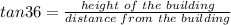
Let's plug in the data to the function above and solve for the height of the building.
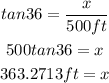
Therefore, the height of the building itself is 363.2713 ft.
Moving on to the height of the building + lightning rod, use the tangent function still but this time, use the 38-degree angle.
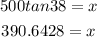
Therefore, the height of the building + lightning rod is 390.6428ft.
So, to determine the height of the lightning rod only, let's subtract the two calculated heights.
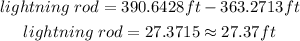
Answer:
The height of the lightning rod is approximately 27.37 ft.