Question

Logan and Rita each open a savings account with a

deposit of $8,100. Logan's account pays 5% simple interest
annually. Rita's account pays 5% interest compounded
annually. If Logan and Rita make no deposits or
withdrawals over the next 4 years, what will be the
difference in their account balances?




Select one
$125.60
$104.05
$113.22
$134.98

Answer 1

For Logan

Principal (P) = $8,100

Rate (R) = 5%

Time (T) = 4 years

The Interest

`\begin{gathered} Simple\text{ }Interest=(PRT)/(100) \\ Simple\text{ }Interest=(8100*5*4)/(100) \\ Simple\text{ }Interest=1620 \end{gathered}`

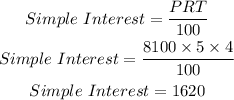
The balance in logan account will be

`\begin{gathered} Amount=Principal+SimpleInterest \\ Amount=8100+1620 \\ Amount=9720 \end{gathered}`

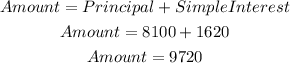
The amount is $9,720

For Rita

Note: Compound Interest Formula

Using the above formula, we have

`\begin{gathered} Amount=P\left(1+r\right)^t \\ Amount=8100\left(1+0.05\right)^4 \\ Amount=8100\left(1.05\right)^4 \\ Amount=9845.600625 \end{gathered}`

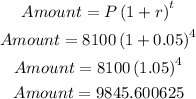
The balance in Rita account is $9,845.60 (to two decimal places)

Therefore, the difference in their account balances is

`\begin{gathered} 9845.60-9720 \\ 125.60 \end{gathered}`

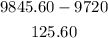
Therefore the answer is $125.60