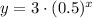Question

PLSSSS PLSSS HELPPPP Use a Calculator to find the equation which models the exponential which models the exponential data given by the table x -2 -1 0 1 2 3 y 12 6 3 3/2 3/4 3/8 answers a y=0.5(3)^x B y=3(0.5)^x c y= 1.5(3)^x d y=3(1.5)^x

Answer 1

Exponential Equation

We are given the following values of x and y:

x={-2,-1,0,1,2,3}

y={12,6,3,3/2,3/4,3/8}

It's required to find the equation that models the table.

The model to use is exponential, which general formula is:

`y=A\cdot r^x`

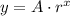
Where A and r are values to determine with the data provided in the table.

Let's use the first two values: x=-2, y=12:

`12=A\cdot r^(-2)`

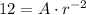
Now use the second pair: x=-1, y=6

`6=A\cdot r^(-1)`

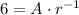
Dividing the second equation by the first:

`\begin{gathered} (6)/(12)=(A\cdot r^(-1))/(A\cdot r^(-2)) \\ \text{Operating and simplifying:} \\ (1)/(2)=r^((-1+2))=r \end{gathered}`

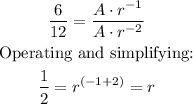
Thus, r = 1/2 = 0.5Thus

Substituting the value of r in any of the two equations (for example the first one):

`12=A\cdot0.5^(-2)`

Operating:

`12=A\cdot4`

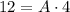
Solving for A:Solving for A

A = 12/4 = 3

Thus, the required equation is:

`y=3\cdot(0.5)^x`

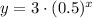
Note we only used two points to determine the equation. The rest of the points from the table should satisfty the equation. We'll only check one of them, for example x=0, y=3

`y=3\cdot(0.5)^0=3\cdot1=3`

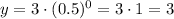
The point satisfies the equation and the rest of the points will also dosfies the equation and

Answer: B

`y=3\cdot(0.5)^x`