Answer: The probability of randomly choosing 2 blue marbles without replacement is
 .
.
B. The probability of getting heads, tails, and heads, in that order when flipping a coin is 1/8.
These events are independent.
Explanation:
Given: The number of blue marbles in the bag = 4
The total number of marbles in the bag =
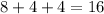
After choosing one marble, the total marbles remains in the bag =

If first marble is blue, then number of blue marbles in bag =
Now, the the probability of randomly choosing 2 blue marbles without replacement is given by :-
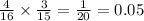
Hence, the probability of randomly choosing 2 blue marbles without replacement is
 .
.
In order when flipping a coin.
Total outcomes = 2
Then, the probability of getting heads, tails, and heads, in that order when flipping a coin is given by :-
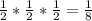
These events are independent of each other because the next event is not affected by the previous event.