Answer:
For a geometric sequence
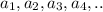
The nth term for this sequence is given by:
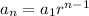 .....[1]
.....[1]
where
 is the first term
is the first term
r is the common ratio
n is the number of terms.
Given the sequence:
80, -160, 320, -640
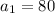
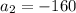
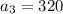
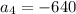
Common ratio(r) is -2
Since,

Substitute the values we have;
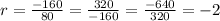
We have to find the next three term of the given sequence:
Using [1] we have
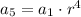
Substitute the given values we have;
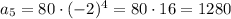
Similarly,
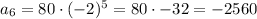
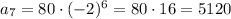
Therefore, next three terms in the given sequence are: 1280, -2560, 5120