From the question
We are given a polygon CDEF
Having the following properties
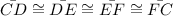
Also, We are given that
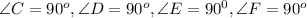
From these given properties we can have the given figure below
From the polygon drawn
We have that the polygon is a SQUARE
Also,
Since a square is a quadrilateral, then the polygon is a QUADRILATERAL
From the given properties
By definition of a rectangle, opposite sides are equal
Hence, a square is a rectangle
Therefore, the polygon can also be a rectangle
Finally, since a parallelogram has opposite sides to be equal, then the described polygon