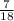Question

Henry rolls 2 number cubes numbered 1 through 6 while playing his favorite board game. He will get a second turn if he rolls a sum that is an even number less than 10. What are Henry's chances of getting a second turn when he rolls the number cubes? 7/18 11/18 5/36 17/36 I got 5/18. I added up the amount of different ways to get 2-8. I found 10. Either the test is wrong or I'm really bad at counting, and I'm not confident enough to count either of them out.

Answer 1

First of all, we know that each cube can land in 6 different ways,
so two cubes can land in (6x 6) = 36 different ways.

Now let's check your count. How many ways can you roll a 2, 4, 6, or 8 ?

Cube-A Cube-B
1 1 2
1 3 4
3 1 4
2 2 4
1 5 6
5 1 6
2 4 6
4 2 6
3 3 6
2 6 8
6 2 8
3 5 8
5 3 8
4 4 8

I get 14 ways.

So the probability of success is

(number of successful ways) / (total possible ways) =

(14) / (36) = 7/18 .

Answer 2

Answer:
`(7)/(18)`

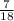
Explanation:

The sample size n ( total pairs )=
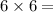`6*6=`36

Pairs having the even sum less than 10 area

(1,3), (3,1), (1,5), (5,1),(3,5),(5,3),

(2,4), (4,2), (2,6),(6,2),

(1,1),(3,3),(2,2),(4,4)

The number of ways to get a sum that is an even number less than 10= 14

The chances of getting a second turn when he rolls the number cubes=
`=\frac{\text{favourable outcomes}}{\text{Total outcomes}}(14)/(36)=(7)/(18)`

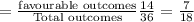
Hence, The chances of getting a second turn when he rolls the number cubes=
`(7)/(18)`