Question

Use special right triangle ratios to find the length of the hypotenuseA. 15 square root 3B. 30C. 15D. 15square root 2

Answer 1

Step-by-step explanation

To find the length of the hypotenuse using the right triangle ratio

Since the angles are in the ratio

`45^0,45^0,90^0`

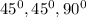
So the side ratio will be in the ratio

`1\colon1\colon\sqrt[]{2}`

Thus,

If x = 15 and the hypotenuse is y

Then

`\begin{gathered} 45^0\colon45\colon90^0 \\ 15\colon x\colon y \\ 1\colon1\colon\sqrt[]{2} \end{gathered}`

Thus, from the above relationship

`\begin{gathered} x=15 \\ y=15*\sqrt[]{2}=15\sqrt[]{2} \end{gathered}`

Therefore, the hypotenuse is

`15\sqrt[]{2}`