Question

How do I write an expression with a negative exponent that has a value between 0 1/2

Answer 1

Something between 0 and 1/2...how about 1/4?
To write this with a negative exponent...
If you have some number with a negative exponent
`n^(-x)`, you can rewrite it as
`(1)/(n^x)` (and vice versa)
Here's how we work the negative exponent on this one:
`\frac14=\frac1{2^2}=\boxed{2^(-2)}`

Answer 2

For this case, the first thing we must do is define variables.
We have then:
b: base of the expression
n: exponent of the expression (<0)
Writing the expression we have:

`b^n`
We want a number between 0 and 1/2
Therefore, for b = 2 and n = -2 we have:

`2^(-2)`
Rewriting the expression:

`(1)/(2^2)`

`(1)/(4)`

`(1)/(4)=0.25`
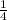
Answer:
an expression with a negative exponent that has a value between 0 and 1/2 is:

`2^(-2)`