Question

The yard behind the Cindy’s house is rectangular in shape and has a perimeter of 72 feet. If the length l of the yard is 18 feet longer than the width w of the yard, what is the area of the yard, in square feet?

Answer 1

`2187\text{ ft}^2`

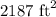
Explanation:

Let l be the length and w be the width of yard behind Cindy's house.

We have been given that the length of the yard is 18 feet longer than the width of the yard. We can represent this information in an equation as:

`l=w+18...(1)`

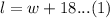
We have been also given that the perimeter of the yard is 72 feet. Since perimeter of a rectangle is 2 times the sum of its length and width, so we can represent this information in an equation as:

`2(l+w)=72...(2)`

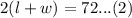
Dividing both sides of equation (2) by 2 we will get,

`l+w=36...(2)`

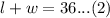
Substituting equation (1) in equation (2) we will get,

`w+18+w=36`

`2w+18=36`

`2w+18-18=36-18`

`2w=18`

`(2w)/(2)=(18)/(2)`

`w=9`

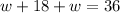
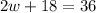
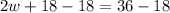
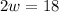
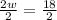
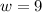
Upon substituting
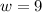`w=9` in equation (1) we will get,

`l=9+18`

`l=27`

`\text{Area of rectangle}=l\cdot w`

`\text{Area of rectangle}=27\text{ yards}\cdot 9\text{ yards}`

`\text{Area of rectangle}=243\text{ yards}^2`

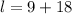
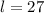
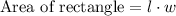
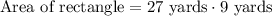
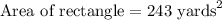
Now, we need to convert the area of rectangle form square yards to square feet.

`1\text{ yards}^2=\text{9 foot}^2`

`243\text{ yards}^2=243* \text{9 foot}^2`

`243\text{ yards}^2=2187\text{ foot}^2`

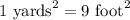
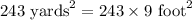
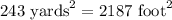
Therefore, the area of yard behind Cindy's house is 2187 square feet.

Answer 2

let
L----------> the length of the yard
W--------> the width l of the yard

we know that
the perimeter is equal to

`P=2*[W+L]`

`72=2*[W+L] \\ 36=W+L` --------> equation 1

`L=W+18` ------> equation 2
substitute equation 2 in equation 1

`36=W+18+W \\ 36=2W+18 \\ W=(36-18)/2`

`W=9 ft`

`L=W+18 \\ L=9+18 \\ L=27 ft`

we know that
Area of the rectangular yard is equal to

`A=L*W \\ A=27*9 \\ A=243 ft^(2)`