Given:
The number of choco bars = 4.
The number of ice creams = 4.
Aim:
We need to find the probability of sequentially choosing 2 choco bars and 1 ice cream.
Step-by-step explanation:
The total items in the box =4+4 =8.
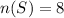
Let A be the event that chooses 2 choco bars.
There are 4 choco bars in the box.
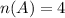
The probability of choosing 2 choco bars.
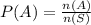
Substitute known values,
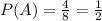
After taking 2 chocobars, the number of items in box = 8-2 =6.
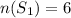
Let B be the event that takes one ice cream from the box.
There are 4 ice creams in the box.
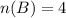
The probability of choosing one ice cream.
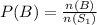
Substitute known values.
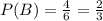
The probability of sequentially choosing 2 choco bars and 1 ice-cream
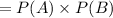
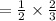
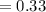
Final answer:
The probability of sequentially choosing 2 choco bars and 1 ice cream is 0.33.