Question

Given a triangle with a=16, A=13°, and B=44°, determine c using the Law of Sines.(round answer to 2 decimal places)

Answer 1

Given the triangle ABC

We know that:

side a=16

∠A=13º

∠B=44º

The law of sines state that the division of the opposite line of an angle and its sine is equal for the three sides of the triangle. So given a certain triangle:

The law of sin states that:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

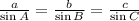
side a divided by sinA is equal to side b divided by sinB and is also equal to side c divided sinC.

Using the given information you have to determine the side length of c, using the equality above we can say that:

`(a)/(\sin A)=(c)/(\sin C)`

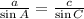
→The measure of angle C is not given but we know that the sum of all interior angles of a triangle is equal to 180º, so using the values of A and B we can determmine the measure of C:

`\begin{gathered} A+B+C=180º \\ 13º+44º+C=180º \\ 57º+C=180º \\ C=180º-57º \\ C=123º \end{gathered}`

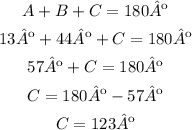
Now that we know the measure of ∠C, along with the measure of ∠A and side a, we can calculate side c:

`\begin{gathered} (a)/(\sin A)=(c)/(\sin C) \\ (16)/(\sin13)=(c)/(\sin 57) \\ c=((16)/(\sin13))\cdot sin57 \\ c=59.65 \end{gathered}`

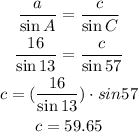
Side c has a length of 59.65