This representation is fine for your purposes - no need to use the completed square form.
To arrive at this solution, you should set the expression (x^2-6x+18) equal to 41, and solve the resulting quadratic. Subtract 41 from both sides to get x^2-6x-23, and from there, apply the quadratic formula to get:
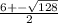
, or
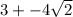
. The line intersects the parabola at two points,

and
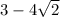
.