Question

Using the completing-the-square method, find the vertex of the function f(x) = 5x2 + 10x + 8 and indicate whether it is a minimum or a maximum and at what point.

a. maximum (1,8)
b. minimum (1,8)
c. maximum (-1,3)
d. minimum (-1,3)

Answer 1

The vertex form is a(x-h)²+k, where (h,k) are the coordinates of the vertex.


`f(x)= \\ 5x^2+10x+8= \\ 5(x^2+2x)+8= \\ 5((x^2+2x+1)-1)+8= \\ 5((x+1)^2-1)+8= \\ 5(x+1)^2-5+8= \\ 5(x+1)^2+3`

The coordinates of the vertex are (-1,3).

The coefficient of x² is positive, so the parabola opens upwards and the vertex is the minimum of the function.

The answer is d.

Answer 2

Answer : d. minimum (-1,3)

`f(x) = 5x^2 + 10x + 8`

The vertex form of quadratic function is

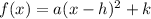`f(x) = a(x-h)^2 + k`, where (h,k) is the vertex

To get vertex form we apply completing the square method

To apply completing the square method , there should be only x^2

So we factor out 5 from from first two terms

`f(x) = 5(x^2 + 2x) + 8`

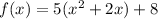
Now we take the number before x (coefficient of x) and divide by 2

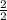`(2)/(2)` =1

Now square it

`(1)^2 =1`

Add and subtract 1 inside the parenthesis

`f(x) = 5(x^2 + 2x + 1 - 1) + 8`

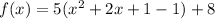
Now we take out -1 by multiplying 5

`f(x) = 5(x^2 + 2x + 1) -5 + 8`

`f(x) = 5(x^2 + 2x + 1) + 3`

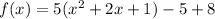
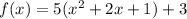
Now we factor x^2 +2x+1 as (x+1)(x+1)

`f(x) = 5(x+1)(x+1) + 3`

`f(x) = 5(x+1)^2 + 3`

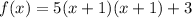
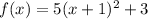
h=-1 and k=3

So vertex is (-1,3)

When the value of 'a' is negative , then it is a maximum

When the value of 'a' is positive , then it is a minimum

`f(x) = 5x^2 + 10x + 8` is in the form of
`f(x) = ax^2 + bx + c`

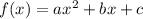
The value of a is 5

5 is positive so it is a minimum

f(x) is minimum at point (-1,3)