Question

Trevor solved the system of equations below. What mistake did he make in his work? 2x + y = 5 x − 2y = 10 y = 5 − 2x x − 2(5 − 2x) = 10 x − 10 + 4x = 10 5x − 10 = 10 5x = 0 x = 0 2(0) + y = 5 y = 5

a. He should have substituted 5 + 2x
b. He combined like terms incorrectly, it should have been 4x instead of 5x
c. He subtracted 10 from the right side instead of adding 10 to the right side
d. He made no mistake

Answer 1

`2x+y=5 \\ x-2y=10 \\ \\ y=5-2x \\ x-2(5-2x)=10 \\ x-10+4x=10 \\ 5x-10=10 \\ \boxed{5x=0} \Leftarrow \hbox{the mistake, it should be 5x=20} \\ x=0 \\ \\ 2(0)+y=5 \\ y=5`

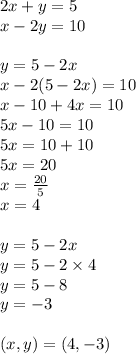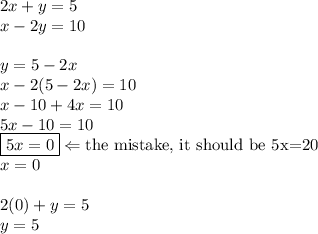
If 2x+y=5, then y=5-2x, so he substituted 5-2x correctly.
x+4x=5x, so he combined like terms correctly.
If 5x-10=10, then 5x=10+10 -> 5x=20, so he subtracted 10 from the right side instead of adding 10 to the right side.

The answer is C.

Here's the correct solution:

`2x+y=5 \\ x-2y=10 \\ \\ y=5-2x \\ x-2(5-2x)=10 \\ x-10+4x=10 \\ 5x-10=10 \\ 5x=10+10 \\ 5x=20 \\ x=(20)/(5) \\ x=4 \\ \\ y=5-2x \\ y=5 - 2 * 4 \\ y=5-8 \\ y=-3 \\ \\ (x,y)=(4,-3)`