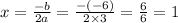The roots of a quadratic equation ax²+bx+c=0 can be determined by calculating the discriminant Δ=b²-4ac.
If Δ>0, there are two distinct real solutions.
If Δ=0, there is one real solution.
If Δ<0, there are no real solutions and two complex solutions.

Δ=0, so there is one real solution. The answer is A.
The solution is: