Question

Use the following sequence to determine the 30th term.15, -85, -185, 285, ...

Answer 1

we have the sequence

15, -85, -185, -285, ...

so

a1=15 first term

a2=-85

a3=-185

a4=-285

Find out the difference between consecutive terms

a2-a1=-85-(15)=-100

a3-a2=-185-(-85)=-185+85=-100

a4-a3=-285-(-185)=-285+185=-100

The difference is a constant

that means ----> this is an arithmetic sequence

where

the common difference d=-100

The formula to calculate the a_n term is given by

`a_n=a_1+d(n-1)`

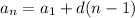
To find out the 30th term

we have

d=-100

n=30

a1=15

substitute

`\begin{gathered} a_(30)=15+(-100)(30-1) \\ a_(30)=15-100(29) \\ a_(30)=-2,885 \end{gathered}`

The 30th term is -2,885