Question

M is the midpoint of CF (line over it) for the points C(3,4) and F(9,8). Find MF

Answer 1

MF = √13 units

Step-by-step explanation:

1- We get the distance between C and F:

The distance formula is as follows:

distance =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

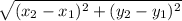
We have:

point C (3,4) and point F (9,8)

This means that:

CF =
`√((8-4)^2+(9-3)^2)`

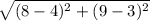
CF = 2√13 units

2- We get MF:

We know that M is the midpoint of CF, this means that:

CM = MF

and

CM + MF = CF

Therefore:

MF would be equal to half CF

MF = 0.5 * 2√13 = √13 units

Hope this helps :)

Answer 2

If M is the midpoint of CF, then the length of MF is half the length of CF.


`C(3,4) \\ x_1=3 \\ y_1=4 \\ \\ F(9,8) \\ x_2=9 \\ y_2=8 \\ \\ \overline{CF}=√((x_2-x_1)^2+(y_2-y_1)^2)=√((9-3)^2+(8-4)^2)= \\ =√(6^2+4^2)=√(36+16)=√(4(9+4))=√(4 * 13)=2√(13) \\ \\ \overline{MF}=\frac{\overline{CF}}{2}=(2√(13))/(2)=√(13)`

The length of MF is √13 units.