
Step-by-step explanation
2 lines are perpendicular if the product ot their slopes equals 1
then,
Step 1
find the slope of the given line
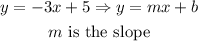
so
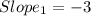
Step 2
Now, let slope2 represents the slope of the line we are looking for ( perpendicular)
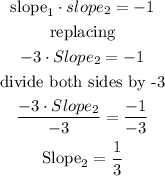
now, check in the answer options the function that has 1/3 as the factor of x
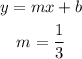
then, the answer is
