Question

The distances (y), in miles, of two cars from their starting points at certain times (x), in hours, are shown by the equations below:

Car A
y = 60x + 10

Car B
y = 40x + 70

After how many hours will the two cars be at the same distance from their starting point and what will that distance be?


a. 2 hours, 150 miles
b. 2 hours, 190 miles
c. 3 hours 150 miles
d. 3 hours, 190 miles

Answer 1

We can simply set the two equations equal to each other:

60x+10=40x+70

We subtract 40x+10 from both sides to get:

20x=60

Divide by 20 to find that x=3. Substitute this back into either equation to find the amount of miles - using the first, 60*3+10=190, so the answer is D.

Answer 2

The correct option is d.

Explanation:

The distances (y), in miles, of two cars from their starting points at certain times (x), in hours, are shown by the equations

Car A:

`y=60x+10` ... (1)

Car B:

`y=40x+70` .... (2)

Equate equation (1) and (2), to find the hours after which the two cars be at the same distance from their starting point.

`60x+10=40x+70`

`60x-40x=70-10`

`20x=60`

`x=3`

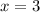
The value of x is 3. It means after 3 hours two cars be at the same distance from their starting point.

Substitute x=3 in equation (1) to find the distance.

`y=60(3)+10`

`y=180+10=190`

The distance is 190 miles.

Therefore option d is correct.