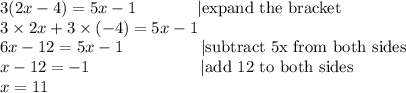Question

Given the equation 5x − 4 = –2(3x + 2), solve for the variable. Explain each step and justify your process.

B. Megan solved a similar equation below. Is Megan's solution correct? Explain why or why not.
3(2x − 4) = 5x − 1
6x − 12 = 5x − 1
11x − 12 = –1
11x = 11
x = 11

Answer 1

A.

`5x-4=-2(3x+2) \ \ \ \ \ \ \ \ \ |\hbox{expand the bracket} \\ 5x-4=-2 * 3x-2 * 2 \\ 5x-4=-6x-4 \ \ \ \ \ \ \ \ \ \ \ \ \ |\hbox{add 6x to both sides} \\ 11x-4=-4 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |\hbox{add 4 to both sides} \\ 11x=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |\hbox{divide both sides by 11} \\ x=0`

B.

`3(2x-4)=5x-1 \\ 6x-12=5x-1 \\ \boxed{11x-12=-1} \Leftarrow \hbox{the first mistake} \\ 11x=11 \\ \boxed{x=11} \Leftarrow \hbox{the second mistake}`

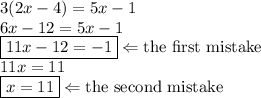
Megan's solution isn't correct.
The first mistake: she subtracted 5x from the right-hand side of the equation, but added 5x to the left-hand side.
The second mistake: she divided the right-hand side of the equation by 11, but didn't divide the left-hand side.

The correct solution:

`3(2x-4)=5x-1 \ \ \ \ \ \ \ \ \ \ \ |\hbox{expand the bracket} \\ 3 * 2x+3 * (-4)=5x-1 \\ 6x-12=5x-1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ |\hbox{subtract 5x from both sides} \\ x-12=-1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |\hbox{add 12 to both sides} \\ x=11`