Question

Find the sum: 1+2+3+ ... +9999+10000.

Answer 1

It's an arithmetic sequence.


`1,2,3,...,9999,10000 \\ \\ a_1=1 \\ d=a_2-a_1=2-1=1`

Find which term is 10000:

`a_n=a_1+d(n-1) \\ 10 000=1+1(n-1) \\ 10000=1+n-1 \\ n=10000`
10000 is the 10000th term.


`S_n=(n(a_1+a_n))/(2) \\ \Downarrow \\ S_(10 000)=(10 000(1+10 000))/(2)=\fra{10 000 * 10 001}{2}=5 000 * 10 001=50005000 \\ \\ \boxed{1+2+3+...+9999+10000=50005000}`

Answer 2

This requires the formula for summation of an arithmetic sequence, which was first derived by Gauss, since the sequence is of the form
`u_(n) = n`.

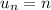
a = 1 (the first term)
L = 10000 (the last term)
n = 10000 (the number of terms summed)

The formula is:

`S = (1)/(2)n(a + L)`

`S = ( (1)/(2)*10000)(1 + 10000) = 50005000`

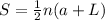
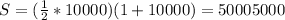
Therefore the sum is 50005000

I hope this helps