Question

Which function has a vertex at the origin? f(x) = (x + 4)2 f(x) = x(x – 4) f(x) = (x – 4)(x + 4) f(x) = –x2

Answer 1

f(x) = –x2

Explanation:

i just did the test and got it right

Answer 2

Answer:
`f(x)=-x^2`

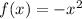
Explanation:

In mathematics,the starting point on a grid is called an origin. It is the point (0,0), where the x-axis and y-axis intercept.

Thus to check which function passing through the origin, we need to check for x=0, y=f(x) must equals to 0.

1.
`f(x)=(x+4)^2`

At x=0,
`f(0)=(0+4)^2=4^2=16`

⇒f(x) is not passing through origin.

2.
`f(x)=x(x-4)`

At x=0,
`f(0)=0(0-4)=0`

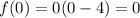
⇒f(x) passing through origin.

But the vertex form of equation is
`f(x)=x^2-4x-4+4=(x-2)^2-4`

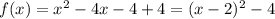
⇒ vertex of f(x)=(2,4)

3.
`f(x)=(x-4)(x+4)`

At x=0,
`f(0)=(0-4)(0+4)=-4*4=-16`

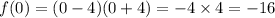
⇒f(x) is not passing through origin.

4.
`f(x)=-x^2`

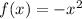
At x=0,
`f(0)=0^2=0`

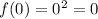
⇒f(x) passing through origin.

Vertex form of equation=
`f(x)=-1(x-0)+0`

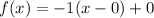
⇒ vertex=(0,0)